目次
はじめに
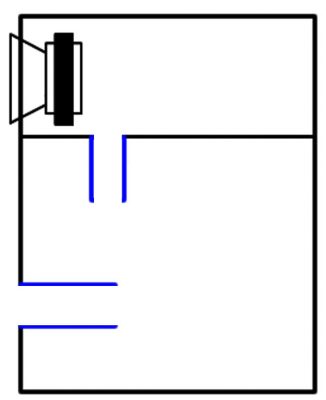
ダブルバスレフ型スピーカーの断面の模式図
前回に続き、ダブルバスレフ型スピーカーについて検討を行います。
→ ダブルバスレフ型スピーカーの実験・研究1(2021年)長岡鉄男先生の公式の検証
今回は、2021年9月に、音楽之友社からontomo mookとして発売されたOM-OF101用のエンクロージャー開発を題材に検討を進めたいと思います。
本エンクロージャーの開発の経緯と概要については、次をご参照ください。
また、OM-OF101ユニットの評価結果については、次をご参照ください。
今回は、特に前回検証を試みた長岡鉄男先生の経験式について、実測値との比較検討から始め、検証を行いたいと思います。
ダブルバスレフ型スピーカーとは
最初に用語等のおさらいをしておきたいと思います。
この項目は、前回と同じです。
ダブルバスレフは、下記の断面図に示すように、エンクロージャー(箱全体)を2つの部屋にわけ、バスレフポートをそれぞれ取り付けて、全体としては、2段階のバスレフポートで構成されるエンクロージャーの形式です。
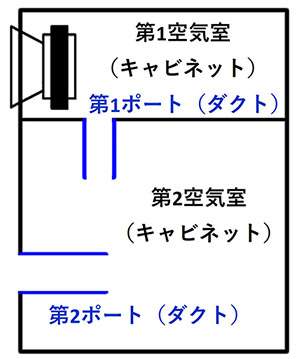
2つの部屋は、それぞれ、スピーカーユニットを取りつけている第1空気室(第1キャビネット)と、第1ポート(第1ダクト)で接続される第2空気室(キャビネット)とから成り、第2空気室(第2キャビネット)から第2ポート(第2ダクト)で外部につながっています。
なお、カッコ内の用語は、長岡先生の著書で用いられている表現で、この場合、意味は同じです。
長岡先生によると、” ダブルバスレフの狙いはローエンドの拡大である ”、とのことです。
1段のみのバスレフで、ローエンドを伸ばすと、途中で音圧の下がった中だるみの領域ができてしまいますが、それを2段階のバスレフポートによって、持ち上げ、平坦に持っていく、というのが目的です。
その狙いのメカニズムを次にもう少し詳しくご説明します。
ダブルバスレフ型スピーカーのインピーダンス特性と周波数特性の特徴
下の図に、ダブルバスレフ型スピーカーの周波数特性(上の曲線)とインピーダンス特性(下の曲線)の例を示します。共に横軸は、周波数で単位は[Hz]です。
最終的には、上の周波数特性と、人の聴力特性などで音は決まるわけですが、スピーカーの設計においては、下の曲線のインピーダンス特性が重要となります。インピーダンスは右側の縦軸の数値となります。
ここでのピークもしくはディップの値が、エンクロージャーの各部屋の容量やポート(ダクト)の容量、それとTSパラメータなどのスピーカーそのものの特性などと関係します。
長岡先生の経験式などは、ある限られた条件内で、これらのピーク値やディップ値を算出できます。
前回の実験の測定例
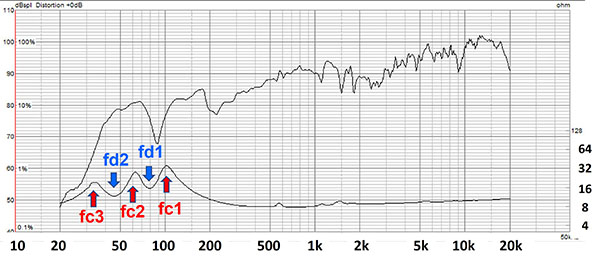
図 1 ダブルバスレフ型スピーカーの周波数特性とインピーダンス特性の例(FE108sol)
上の図は、前回の実験のケースの一つで、ユニットはFE108solでした。
全体に、ハイ上がりな特性といえます。
今回の実験の測定例
今回の、OM-OF101をダブルバスレフエンクロージャーに用いた例を次に示します。
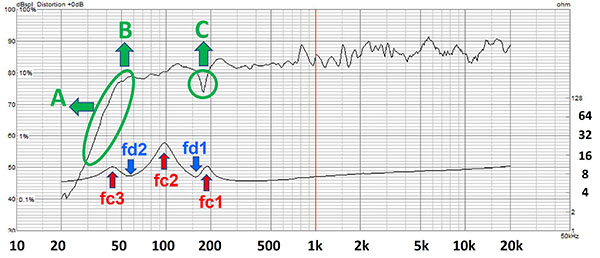
図 2 ダブルバスレフ型スピーカーの周波数特性とインピーダンス特性の例(OM-OF101)
図2の下がインピーダンス特性のグラフです。ここで、ダブルバスレフのインピーダンス特性の特徴である、3つのピーク値と2つのディップ値がでているのがわかります。
今後引用の際の取り決めとして、ピーク値を示す記号を、高い周波数から順番に fc1, fc2, fc3。また、ディップ値は、同様に高い方から、fd1, fd2 とします。
次に、一般的なダブルバスレフの狙いを、図2の上のグラフである周波数特性に緑でA、Bで示しました。
すなわち、目的は、低域の特性をより低い領域まで再生できるようにして、かつ、低域の音圧をあげることです。これができるのはかなり魅力的です。
ところが、ダブルバスレフの場合、Cで示したような、中域にディップができてしまうのが一般的です。
ダブルバスレフ特有の中域のディップ
この発生する要因としては、少なくとも3つ考えられます。
1.もともとのスピーカーの周波数特性の影響
2. バスレフポートから出る特定の周波数領域での逆相成分による音の相殺
3. インピーダンス特性に示されるダブルバスレフの抵抗成分
1が原因となる場合は少ないのですが、2については、ダブルバスレフの原理上ある程度仕方がないようです。この成分については、測定する距離と周波数でも当然かわってきますので、やや厄介でもあります。これを解決するためには、トリプルバスレフにするなどという方法もあるようですが、箱が非常に大きくなるので、あまり現実的ではなさそうです。
現時点で、比較的容易にコントロールできるかもしれないのは、3のインピーダンス特性です。
インピーダンス特性について
インピーダンス特性において、ダブルバスレフの場合、山が3つありますが、通常のバスレフでは2つ、密閉箱では1つ、また、バックロードホーンでは、5つ出たりもします。
これらの場合のインピーダンス特性は、それぞれのダクトに関係した空気抵抗を含むバルクな特性を示していると言えます。
つまり、共鳴等により、振動板が震えやすい場合は、インピーダンスが低く示され、音が出る際の気流抵抗などが大きな場合は、振動しにくいため、インピーダンスが高くなるわけです。
この共鳴とか気流抵抗を生み出すのは、ダクトと内容積などですので、たとえば内容積(比)やダクトの調整などでそれぞれのピークとディップの位置と大きさを変化させることができます。
また、ピークの場合は、スティフネスの計算などで各ユニットの固有の値であるTSパラメータのいくつかも関係します。
これらを上手くコントロールすることで、中域に発生するディップの程度を少なくすることと、低域をもっと伸ばすことが当面の狙いです。
インピーダンス特性の計算
従って、これらについて、まずは経験式等で、それぞれの値の目安が付けることができれば、エンクロージャーの設計に役立ちます。
そのためにも、経験式の適合範囲をまずははっきりとしていく必要があります。
前回の実験では、どうやら諸条件の設定範囲があまりに広く、式に適合するケースのほうが少ない結果となりました。実用的ではなかったとも言えます。
実際のところ、図1のグラフを見ても、いい音はしないだろうと思わせるプロファイルでした。
今回は、より実際的なケースとして各ダクト等を現実的な範囲で設定し、検討します。
図2は、今回検討したケースの一つですが、これを見ると、周波数特性的にはかなり期待できそうです。
なお、この周波数特性のグラフだけでは、わからないのですが、ダブルバスレフにすると、低域の勢いが出てきます。弾んだ低音を再生する事ができます。
バスレフを大型化すると、周波数特性的には、低域が伸びるのですが、やや張りのない、ともすれば低域過剰な音となってしまうのですが、ダブルバスレフは、比較的締まって、かつ伸びやかな低音を得ることができます。
この特性については、別の測定指標で示すことができないか、今後検討していきたいと考えています。
OM-OF101用エンクロージャーを用いた式の検証
検証に用いた公式について
今回も、長岡鉄男先生の式について検証することからまずは始めたいと思います。
検証に用いた公式は、長岡鉄男のオリジナルスピーカー設計術【基礎知識編】のダブルバスレフの項であるp19-p20に示されているのを用いました。また、一部は、密閉型p13、とバスレフp16に記載してある式をもちいています。これらは、ダブルバスレフの項の記載内容に従っています。
実測値の測定方法
先程示した図2の測定結果のグラフを再び示します。ここにあるように、インピーダンスのピーク値である fc1, fc2, fc3とディップ値のfd1, fd2をアプリ上のカーソルで値を測定しました。測定値としては、高さ[Ω]と周波数[Hz] を計測していますが、今回は、周波数についての結果を用います。
なお、ピーク値については、比較的正確な値を取れますが、ディップ値については、付近の最低値をその値としていますが、ピークとピークとの間にあるため、その影響も考えられ、場合によっては真のディップ値からやや外れている可能性もあります。

図 2 ダブルバスレフ型スピーカーの周波数特性とインピーダンス特性の例(OM-OF101)
測定したエンクロージャーについて
今回、24通りに条件を変えてエンクロージャーを作成し、測定しました。
なお、今回ご紹介するのは、同一の外寸のエンクロージャーの結果です。内容積が、約13リットル、内部のダクト等を除いた実効体積は、約12リットルとなります。
ちなみに、今回のOM-OF101用エンクロージャーの検討にあたっては、別ブログでご紹介しているように、4種類の外寸の箱と16Lのバスレフ箱などとを比較検討しています。
変化させたパラメータは、第1空気室と第2空気室との比率、第1ダクトの長さと高さ、また第2ダクトの長さと高さです。なお、内容積は一定ですので、ダクトの変更により、第1空気室と第2空気室とのそれぞれの実効体積と、全体の実効体積(=第1空気室の実効体積+第2空気室の実効体積+第1ダクトの実効体積)は、わずかですが、変化します。
前回の実験とは異なり、今回の設定は、設定範囲を比較的絞った場合となります。この中には、最終的な製品にかなり近い組み合わせも含まれます。
断面図のイメージを下に示します。基本構造は、Z601系の変形ダブルバスレフです。
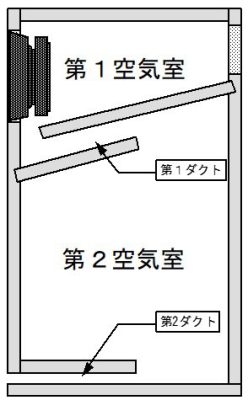
図3 実験用エンクロージャーのイメージ図
ピーク値とディップ値の測定結果
測定結果を下に示します。
各項目を簡単にご説明します。
まず、左から、測定No. これは、試作検討した順番のシリアル番号です。No1-24までありますが、No13については、後で設定値と異なっていたのが判明したので、オミットしています。従って全23データとなります。
次が、第2/第1 比率、第2空気室の実効体積を第1空気室の実効体積で割った値です。
第1ダクトの長さは、短い順に、1-5で表示しました。また、第1ダクトの高さは、低い順(=ダクトが狭い)に、1-6の6段階で示しました。第2ダクトについては、長さが、1-6の6段階、高さが、1-2の2段階です。
測定結果を示します。
表1 測定結果一覧表
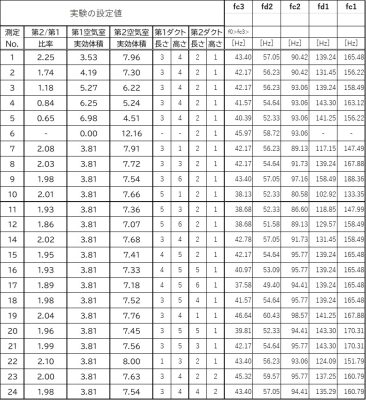
なお、No.6は、第1ダクトを取り外して、第2ダクトのみをシングルバスレフとして動作させたケースです。
このNo6は、シングルバスレフですので、ピークは2つ、ディップが1つとなります。それぞれ、fc3, fc2、fd2として記載しました。
それ以外は、すべて3つのピークと2つのディップがありました。
計算式の結果について
次に、長岡先生の経験式の結果を示します。
各項目は、先程と同様です。
表2 計算結果一覧表
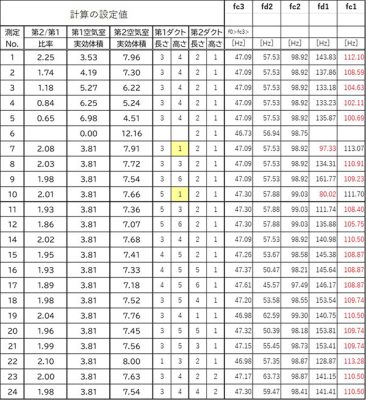
ここで、赤字で示したのは、左側の項の数字よりも、小さな値となったケースです。
本来、周波数の低い順に、fc3、fd2、fc2、fd1、fc1と並ぶはずが、計算結果では、逆転してしまっているケースとなります。
これをみると、fc1では、2例を除いたすべてが、逆転した結果となっています。これは、計算が間違っているか、式がそもそも合っていないかということですが、同じような式から算出されるfc2の値が、後で示すように、実測値とほぼ合っている状況をみると、計算違いということではなさそうです。
また、fc1が逆転していない2例では、fd1の値が、fc2よりも小さいという逆転が生じています。
この2例、No.7とNo.10は、共に、第1ダクトが1で、狭小となっています。このダクトの高さでは、式が想定している条件よりも、第1ダクトでの気流抵抗が大きく、それが誤差として現れていると考えられます。
測定値と計算値との差分の結果の検討
次に、今回の測定値から計算値を引いた差分の一覧表を示します。
表3 測定値と計算値の差分の一覧表
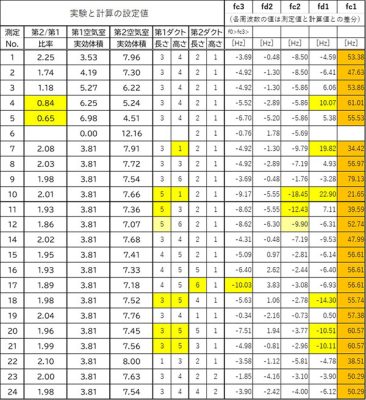
fc1については、そもそも計算値のほとんどがfd1と逆転していますので、かなり大きな差分の値となっています。また、それは逆転していなかったNo.7とNo.10も同様で、すべてオレンジで示しました。
次に、差分の絶対値が10(Hz)以上の部分を目安として黄色で着色しました。
それぞれの値の原因と思われる項目を設定値の項で、同じく黄色で着色しています。
上から順番に検討していきたいと思います。
No.4
まず、No.4ですが、fd1の差分値が10.07となっています。この前後のケースは、No1からNo5までが、第1空気室と第2空気室の比率を変えた場合で、No.6が第1空気室をなくし、バスレフとした場合です。
No.4では、比率が0.84となっており、第1空気室の方が第2空気室よりも大きくなっており、No3以上と逆転しています。ちなみに、fd1の式を下に示します。
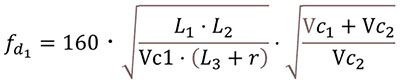
L1: 第1ダクトの高さ、L2:第1ダクトの幅、L3:第1ダクトの長さ(cm)
r:角型ダクトの面積(L1・L2)を円んに換算した時の半径(cm)
Vc1:第1空気室の実効内容積、Vc2:第2空気室の実効内容積(リットル)
ここで示すように、(Vc1+Vc2)/Vc2の平方根の値が積算されていますので、内容積でのVc1とVc2との比率が式の有効範囲に関係して来ている可能性があります。長岡先生は、” 第2空気室の第1空気室の内容積の1.5~3倍ぐらいにとる。” と記載していますので、想定された範囲を超えているために生じた誤差と考えられます。
ただ、興味深いのは、その次のNo.5です。これは、同比率が、0.65と一段と低いにも関わらずNo.3と同等程度で実測値とマッチングしています。No.4とNo5の条件の間に、なんらかの変曲点があるようです。
No.7 とNo.10
次に、No.7とNo.10です。
この2つは、先程の計算結果での判定でも、fc2とfd1との順番が逆になっていたケースでもあります。
fd1の値の差分がそれぞれ、19.82と22.90と乖離しています。
これは、共に第1ダクトの高さが1のパターンであり、ダクト高さが少ないことが原因と考えられます。
ちなみに、長岡先生は、” (第1)ダクト面積は、(ユニットの実効振動面積の)1/4以上としたい、1/3~1/2が手頃だ。” と記載されています。
今回の有効振動板面積は、OM-OF101の有効振動半径が4cmですので、50.27cm2となります。
また、No,7とNo,10の第1ダクトの面積は、14.40cm2ですので、その面積比は、14.40/50.27=0.28となり、1/4=0.25よりはやや大きいですが、推奨の範囲からはずれています。
第1ダクト断面積が、1/3以下なのは、第1ダクト高さのパターン1の、この2つだけでした。
ただし、実際に音を聞いてみると、No,7は、低域がよく弾んだ感じに聞こえ、いい印象を与えます。
第1ダクトの高さが狭く、式と合っていないから音が悪い、というわけでもなさそうです。
このあたりの加減については、今後検討が必要と思います。
No.10, No.11, No,12
この3つは、fc2の差分の値が大きくなっています。
この3つに共通するのは、第1ダクトの長さがパターン5であることです。すなわち一番長い。その中でもダクトの高さが低いNo.10の乖離が最も大きくなっています。
第1ダクトの気流抵抗が式の想定範囲よりも大きくなっていることが原因と思われます。
No.17
このNo.17は、fc3の計算結果と異なっています。最も、この式は不等式で示されています。
本来は、f0>fc3>計算結果 という式ですので、ここでの差分の値はプラスに振れるはずですが、すべて結果がマイナスになっていますので、式の予想とは異なる傾向に一般になってしまっているとは言えます。
ただその中でも、No17が特に乖離が大きい。これは、No.17のみ第2ダクトが一番長く、かつ狭いという条件によるものと考えられます。つまり、第2ダクトの気流抵抗が大きすぎているようです。
No.18,No.20,No.21
この3つのfd1の差分の値が大きくなっています。
これらに共通するのは、第1ダクトの高さが2番めに大きいパターン5で、長さがパターン3ということです。
このダクト高さの場合、ダクト断面積は、38.40cm2となり、ユニットとの比は、0.76で、先程の1/3-1/2(=0.5)のお勧めの範囲より大きな方向にずれています。
第1ダクトの断面積がこのケースの場合、大きすぎているようです。
かつ長さも比較的短いため、第1ダクトでの気流抵抗が小さすぎて、全体としてはシングルバスレフのような動作に近づいている可能性があります。
なお、これらより大きなパターン6がNo12ですが、これのfd1の差分は、-6.31と比較的小さくなっています。
これは、No.12の第1ダクトの長さが、最も長いパターン5のため気流抵抗が大きくなり第1ダクトとして機能しているためと思われます。
まとめ
オンキョーのOM-OF101用のエンクロージャーを用いて、長岡鉄男先生の経験式の計算結果と実際の測定結果とを比較しました。
その結果、fd1、fd2とfc2については、長岡先生の想定していた範囲において、経験式で得た値と実測値とがかなり近い値となりました。また、不等式で示されているfc3も比較的近い値が得られています。
しかしながら、fc1については、実測値との間に乖離がかなりあり、かつ本来 fd1<fc1 であるはずが、今回設定のほとんどの場合において、fd1>fc1 という計算結果になっています。
このfc1の計算式については、今後の大きな検討課題と思われます。
以上により、fd1、fd2とfc2、fc3の4つについては、長岡先生の想定していた適用範囲において、公式により、各値を推定することができることがわかりました。
なお、今回は詳細を記載していませんが、今回の実験の結果、中域のディップの低減化が、ある程度できることがわかってきました。
また、同容量のシングルバスレフと比べ最低域はほぼ同等で、40Hz付近の再生が可能となっています。
さらに低音の質が向上し、シングルバスレフに比べ弾む感じに聞こえます。その結果、一段とバランスの良い音質を得ることができました。