目次
はじめに
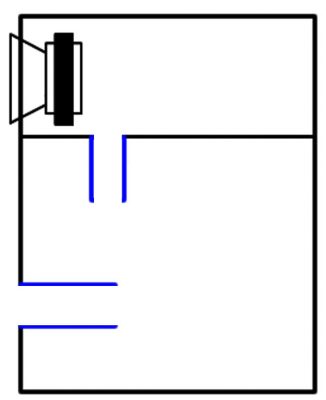
ダブルバスレフ型スピーカーの断面の模式図
今回は、ダブルバスレフ型スピーカーについて検討をしていきたいと考えています。ダブルバスレフは、構造がそれほど複雑ではないのですが、その動作(音)の予想が難しく、設計が容易ではありません。
設計の式を日本語で検索した場合は、長岡鉄男先生の経験式が、多くの場合まず出てきます。
ただ、長岡先生自らが述べられているように、” 一見単純な箱のようだが、動作はバックロードホーンよりも複雑であり、、中略、、カンと経験でなんとか設計している。” とのことでなかなか敷居が高いのが現実です。
今回は、以前に音工房Zで行った実験結果を改めて検討することから、まずは始めていきたいと思います。
ダブルバスレフ型スピーカーとは
ダブルバスレフは、下記の断面図に示すように、エンクロージャー(箱全体)を2つの部屋にわけ、バスレフポートをそれぞれ取り付けて、全体としては、2段階のバスレフポートで構成されるエンクロージャーの形式です。
2つの部屋は、それぞれ、スピーカーユニットを取りつけている第1空気室(第1キャビネット)と、第1ポート(第1ダクト)で接続される第2空気室(キャビネット)とから成り、第2空気室(第2キャビネット)から第2ポート(第2ダクト)で外部につながっています。
なお、カッコ内の用語は、長岡先生の著書で用いられている表現で、この場合、意味は同じです。
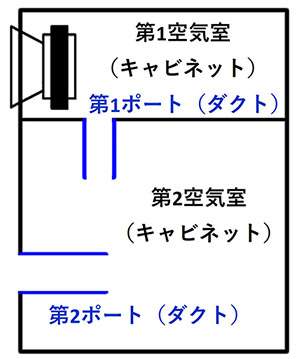
長岡先生によると、” ダブルバスレフの狙いはローエンドの拡大である ”、とのことです。
1段のみのバスレフで、ローエンドを伸ばすと、途中で音圧の下がった中だるみの領域ができてしまいますが、それを2段階のバスレフポートによって、持ち上げ、平坦に持っていく、というのが目的です。
その狙いのメカニズムを次にもう少し詳しくご説明します。
ダブルバスレフ型スピーカーのインピーダンス特性
下の図に、ダブルバスレフ型スピーカーの周波数特性(上の曲線)とインピーダンス特性(下の曲線)を示します。共に横軸は、周波数で単位は[Hz]です。
最終的には、上の周波数特性と、人の聴力特性などで音は決まるわけですが、スピーカーの設計においては、下の曲線のインピーダンス特性が重要となります。インピーダンスは右側の縦軸の数値となります。
ここでのピークもしくはディップの値が、エンクロージャーの各部屋の容量やポート(ダクト)の容量、それとTSパラメータなどのスピーカーそのものの特性などと関係します。
長岡先生の経験式などは、ある限られた条件内で、これらのピーク値やディップ値を算出できます。
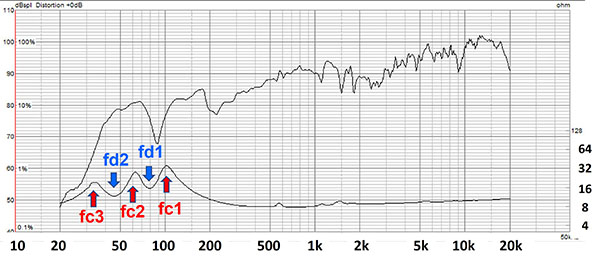
図 ダブルバスレフ型スピーカーの周波数特性とインピーダンス特性の例
ここで示すように、ダブルバスレフのインピーダンス特性では、3つのピーク値と2つのディップ値がでるのが大きな特徴です。ピーク値を示す記号として、高い周波数から順番に fc1, fc2, fc3。また、ディップ値は、同様に高い方から、fd1, fd2 とします。
ざっくりと言えば、インピーダンスは、交流での電圧/電流の比ですから、インピーダンスが低いと、同じ電圧であれば、電流がたくさん流れるわけです。つまりインピーダンスが低いほうが見かけの電力が大きくります。今回、低域での音圧を上げたいわけですから、ディップの値であるfd1とfd2の値を調整することで、狙った領域の低域での音圧を高くする、というのが最終的な目的となります。
一方、ピーク値による出力の低下もあるので、それらとの兼ね合いをスピーカーユニット毎に追い込んでいくということになります。
まずは経験式等で、これらの値の目安が付けることで、エンクロージャーの設計に役立てることができるわけです。
そのためにも、経験式の適合範囲をまずははっきりとしていく必要があります。
ダブルバスレフの実験と結果
実験内容
以前行った実験の詳細については、下記のリンク先にあります。
上に示したダブルバスレフの概念図にある4つのパラメータを、それぞれ2つまたは3つ設定した箱を再現し、それぞれの周波数特性とインピーダンス特性を測定しました。
4つのパラメータと設定値は下記となります。
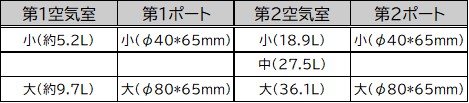
なお、この段階では、長岡先生の経験式の前提条件等は考慮していません。
したがって、あとで、算出した場合、そもそも前提条件と合っていなかったということもあるかもしれません。
ただ、前提条件が文章だったり、**倍といった表現だったりもするので、そもそもの数値的な前提条件を探るという作業も必要かとも思われます。
今回行った実験は、弊社で2016年に行った24パターンのダブルバスレフで実際に測定したインピーダンスと、長岡鉄男先生が出している本にだしているダブルバスレフのシュミレーションがどれくら合うか(近いか遠いか)を調べる実験です。
実験の組み合わせ
前記の条件の組合せは、2×2×3×2=24通りとなります。
それぞれを ”測定No.” という名称で、1-24まで設定しました。
一覧表が下記となります。
表 本実験の設定条件一覧表
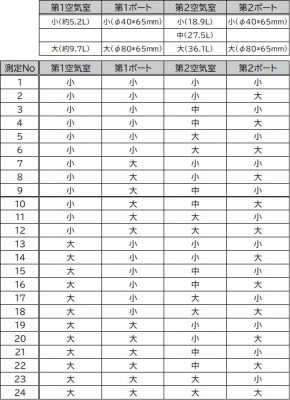
実験結果
インピーダンス特性の測定結果から、測定に用いたアプリのカーソル機能により、各ピークとディップの周波数を測定して特性値としました。一覧表を下記に示します。
各測定結果は、ピークの大小やカーブのなだらかさ加減など異なる点はありますが、全て ”fc3<fd2<fc2<fd1<fc1" というピークとディップが観測できました。
表 本実験結果の各ピークとディップの周波数の値
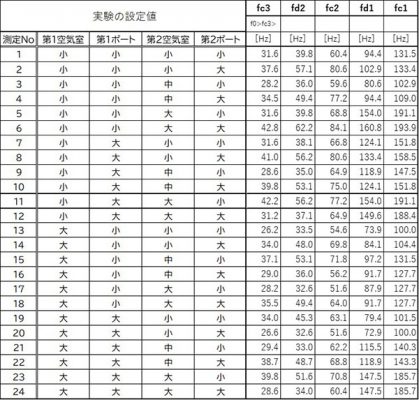
*これらのデータを引用先にアップします。
計算式の結果
今回の測定にあたってはスピーカーユニットとしてFostexのFE108solを用いました。
FE108solの諸特性の一覧表を示します。
表 FE108solの諸特性
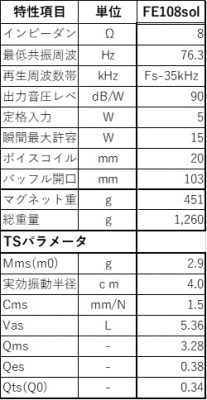
次に、長岡先生の計算式による各条件に対応する計算結果の一覧表を下記に示します。なお、各式の詳細については、長岡鉄男のオリジナルスピーカー設計術[基礎知識編]p19-p20をご覧ください。
ここで、ピークを算出する式とディップを算出する式とでは、用いるパラメータが異なります。
後者のディップの式が、エンクロージャとダクトの容量により算出されるのに対し、前者は、ユニットとキャビネットとダクトのスティフネスが式に入ってきます。ユニットのスティフネスには、f0とm0の値が計算式に入ります。
表 各値の計算結果の一覧表
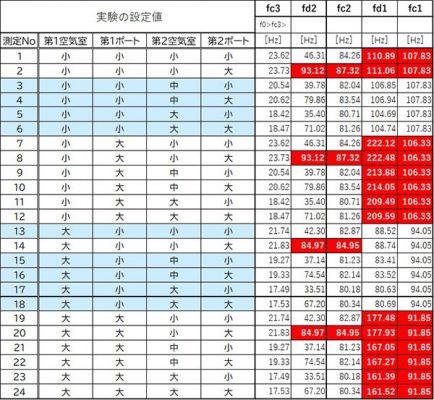
ここで、計算結果の赤の着色の白抜き文字の部分は、本来の周波数の順番である ”fc3<fd2<fc2<fd1<fc1" と順番が入れ替わっている部分です。逆に条件の青の着色は、順番通りとなります。順番通りが、9個という結果となりました。
次に、実測値と計算値の差分の一覧表を示します。
表 各値の実測値と計算式の差分の一覧表
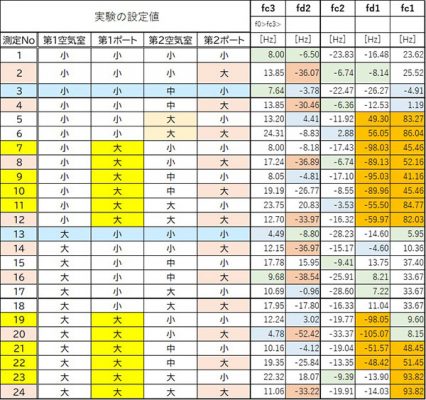
ここで、fc3、fd2、fc2、fd1、の各項目には実測値と計算値の差分の値を記載しています。差分結果は、(実測値ー計算値)で算出しています。
目安として、差分の絶対値が5以下を青、10以下を緑で着色しました。
また、fc1とfd1では、差分の絶対値が40以上の大きな値についてオレンジに着色しました。
f d2では、差分の絶対値が30以上の場合について薄い赤で着色しました。
結果の考察
次に、先に得られた結果について、検討します。
まず、最後に示しました各値の実測値と計算式の差分の一覧表の結果についてです。
それぞれの値について個別に見ていきます。
まず、fc1とfd1の差分の大きくなった組合せですが、これは、第1ポートが”大”の場合にほぼ対応しているようです。どうやら今回選定した第1ポートの大の場合は、式の適合範囲から出ているようです。
また、同様に、第2ポートが”大”の場合は、fd2の値がずれています。こちらも、経験式の適応範囲からは出てしまっているようです。
また、第2空気室が”大”の場合も、fc1、または、fd1が合わなくなっているようです。このケースは、5と6,11と12,17と18,23と24となりますが、例外は、17と18のみで、他は似たようなインピーダンス特性の形状と傾向を示しています。
特にfc1の値が、fc2に比べ200Hz近くとかなり高い周波数で、かつインピーダンスの山が低くなっているのが共通した特徴です。
例として、ケース5とケース6の周波数特性とインピーダンス特性を示します。
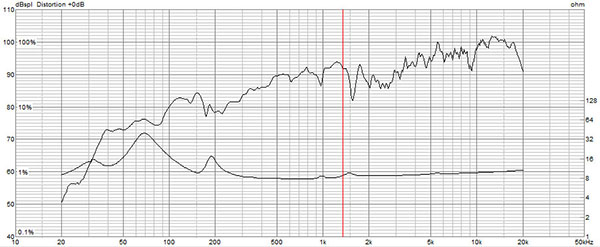
図 ケース5の周波数特性とインピーダンス特性
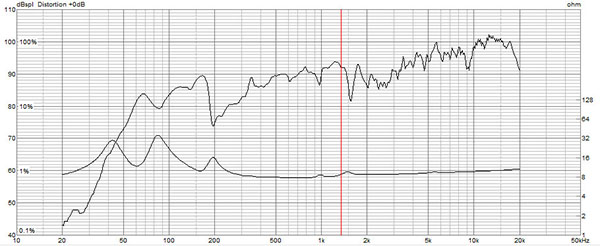
図 ケース6の周波数特性とインピーダンス特性
例外であるケース17と18の共通点は、第1空気室(大)に、第1ポート(小)であることで、fc1の値は全く同じ値の、127.7Hzとなっています。
同じスピーカーユニットを用いていますから、経験式からは、ケース17と18のfc1の結果は同じで、合っています。
次に、ケース18は第2ポートが大で、ダブルバスレフのインピーダンス特性として典型的な3つのはっきりとした山を持っていますが、ケース17は、第2ポートが小で、fd2の値がかなり小さく、fc3のピークも低く小さくなっています。
今回の実験においては、ポートの長さは一定で、開口断面積の大と小で、各ポートの大、小を区別しています。
fd2の経験式では、開口断面積/ポート長さの比が大きいほど、周波数が高くなるので、今回の場合は、ポート大の方が、容積が大きくなりますが、断面積が大きいため、fd2の周波数の値は大きくなります。
逆に、開口断面積を一定にして、ポートの長さでポートの容量の大小を設定した場合は、容積の大きなポートの長い方が、fd2の周波数の値が低くなります。
ケース17とケース18についてそれぞれ示します。
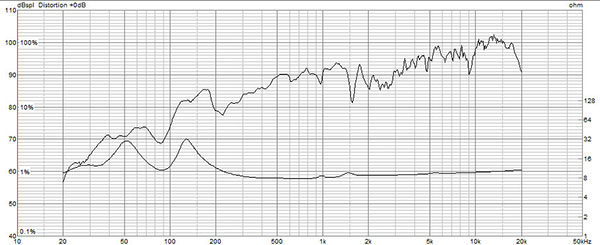
図 ケース17の周波数特性とインピーダンス特性
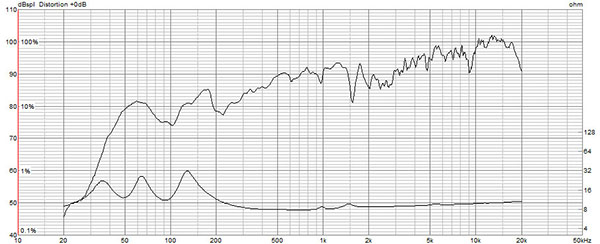
図 ケース18の周波数特性とインピーダンス特性
第2ポート大のケース18の方が、fd2の周波数の値が小さいのがわかります。またこちらは典型的なダブルバスレフのインピーダンス特性である3つの山がはっきりとしています。
ケース17では、fd2の実測値が、32.6Hzとかなり低くなっており、おそらくそのためfc3のピークはかなり判別しにくくなっていると思われます。実験用の設定値としては、第2ポートによる共振周波数の値がやや低すぎたということかと思われます。
ただし、この2つについては、経験式から推定される動作と実測値の動作傾向が一致しているようです。
まとめ
ダブルバスレフ型の動作試験用エンクロージャーを作成し、スピーカーユニットにFostexのFE108solを用いて、各構成要素の値を組合せ、ダブルバスレフスピーカーの動作について検討しました。
今回は、第1回として、各条件を大きく振り、全体の動作傾向をみることを大きな目的としました。
実験としては、構成要素として、第1空気室を2つ、第1ポートを2つ、第2空気室を3つ、第2ポートを2つ、それぞれ組合せ24通りの組合せについて、エンクロージャーを設定し、各々の周波数特性とインピーダンス特性を測定しました。
さらにダブルバスレフのインピーダンス特性に特徴的な3つのピークと2つのディップについて、周波数の高い方から、それぞれfc1、fc2、fc3と、fd1、fd2として、実測することで測定値を得て、特性値としました。
一方、長岡鉄男氏の経験式によって各々の値を算出し、比較しました。その結果、今回の設定範囲においては、式に適合する場合が少ないという結果を得ました。
想定される原因としては、特に、今回用意した第1ポートと第2ポートの条件がそれぞれ経験式の適合範囲から、かなりのケースが、はずれてしまっているためと思われます。
ただし、比較的適合しているケースもあり、また、各設定条件の違いによる特性値の相違を経験式に基づき、その傾向をよみとることもできました。
今後、各構成要素の設定範囲をより最適化した上で、各々の条件設定を行い、あらたな実験を行うとともに、各特性の測定結果と試聴結果との比較検討も行っていきたいと考えています。